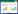2. 邯郸市紧急救援指挥中心, 邯郸 056002
2. Handan Emergency Medical Command Center, Handan 056002, China
院前急救护理是急救医疗服务(emergency medical services, EMS)体系的重要组成部分, 是衡量社会整体医疗服务水平的重要指标[1], 在挽救生命和降低伤残率方面起着关键作用, 对于重症和受伤患者, 在院前迅速采取行动尤为重要[2]。院前急救服务由政府主办, 作为社会保障体系不可或缺的环节, 直接关系到人民群众的生命安全。掌握院前急救医疗服务需求的趋势, 及时预测救护车需求, 有助于优化急救医疗资源的合理配置, 从而减少响应时间和资源浪费[3-4]。在需求高峰期, 确保充足的应急人员和设备配置, 在低需求期优化资源利用, 减少调度准备和响应时间[5]。预测正日益凸显其不可或缺的重要性, 它们是生存的标志和世界上的商业语言[6]。目前, 呼叫量到达、救护车需求和急诊科预测等领域受到了极大的关注[7]。
时间序列预测模型是基于历史数据的数学技术来预测需求[6], 较为常见有ARIMA模型[8]、线性趋势季节模型[9]、指数模型[10]、Prophet模型[11]等。ARIMA是一个简单、精确和低成本的预测模型, 适用于短期预测, 能够产生可靠的预测值, 因此对公共卫生预警监测产生了积极影响[12]。线性趋势季节模型因其易于理解被应用于医学各个领域如院前急救出车车次[13], 但在处理时间序列的非线性部分存在一些局限性[14]。指数模型是一种特殊的加权移动平均法, 其特点在于加强了近期观察值对预测值的作用, 不同数据的权重根据时间上的距离进行加权, 权重呈指数衰减[10]。它通过预估特定的参数来进行预测, 该模型较适合短期预测[8]。Prophet是一种相对较新的模型, 自推出以来, 该模型已广泛用于医学研究和其他领域[15]。Prophet模型能够自动检测数据线性或非线性趋势, 并识别和调整异常值, 处理趋势随时间变化的情况, 防止它们影响预测结果[16]。然而, 单一模型可能无法充分利用数据的所有特征, 导致预测性能受限。集成模型结合了不同模型的优点, 可以提高预测精度[17]。相关研究人员对中国大陆季节性流感进行预测, 得出混合模型比单一模型性能更好, 能较好的拟合出和真实数据一致趋势[18]。另外, 在当前研究领域中, 尚无专门针对邯郸市院前急救出车车次预测的研究。基于此, 本研究通过应用ARIMA模型、线性趋势季节模型、指数模型、Prophet模型进行拟合预测, 并基于单一模型进行集成, 开发了最优集成模型Lpro, 以提高预测的准确度和可靠性, 进而为邯郸市院前急救人员配置、优化调度提供科学依据。
1 资料与方法 1.1 研究对象本研究所使用的数据资料来源于邯郸市紧急急救指挥中心2019—2023年院前急救业务统计数据库, 共获得记录324 799条, 过滤缺失重复等记录后, 剩余289 949条数据。其中, 2019—2022年各年出车总数分别为35 527例、52 015例、61 836例和66 540例, 总计215 918例。2023年出车总数为74 031例, 用于模型验证。在数据处理方面, 利用Python 3.10.7版本, 按照年份、月份对有效出车车次进行了详细统计。
1.2 研究方法 1.2.1 时间序列模型ARIMA模型适合各领域的时间序列分析, 模型包含三个关键部分: 自回归模型(AR)、移动平均模型(MA)和季节性ARIMA模型(SARIMA)[19]。其中, AR模型表示当前观察值与之前观察值之间的关系; MA模型用于捕捉残差的特征, 它考虑了过去的预测误差对当前值的影响; SARIMA在ARIMA模型基础上考虑了季节性成分。分析过程中可以应用auto.arima()函数选择出最佳的ARIMA模型阶数, 极大地简化了时间序列预测模型的建立过程。
线性季节趋势模型[20]考虑了数据的季节性、趋势性和周期性, 且便于计算和理解, 适用于具有明显季节周期性和长期趋势特征的数据。计算过程主要分为如下步骤: 应用趋势剔除法计算季节指数、构建线性回归模型$\hat{y}_{i}=a+b t_{i}$求解长期趋势预测值。其中, $\hat{y}_{i}$为预测值; a为截距; b代表趋势斜率, 表示平均增长量; ti为时间变量, 通常取其编号1, 2, 3......, n。然后利用最小二乘法原理, 求解参数。
Prophet模型是一种基于加法模型的自动预测时间序列和未来趋势的方法[21]。该模型适用于具有趋势和季节性变化的数据, 是一种用于时间序列预测的模型。时间序列通常由趋势项、季节项、节假日项和残差项组成。Prophet模型通过将这些组成部分结合在一起, 捕捉数据中的长期趋势、季节性波动以及节假日效应, 从而提供准确的预测结果。一般形式为: $\hat{y}(\mathrm{t})=\mathrm{g}(\mathrm{t})+\mathrm{s}(\mathrm{t})+\mathrm{h}(\mathrm{t})+\epsilon_{t}$, 其中, 趋势模型g(t)体现非周期变化趋势, 自动检测并适应时间序列的趋势变化; 季节性s(t)使用傅里叶级数来适应年度、月度、周度、日度的周期变化; 假期效应h(t)体现节假日对预测值造成的影响; $\epsilon_{t}$表示噪声项。
指数模型是一种比较常见的模型, 分为单指数平滑法、双指数平滑法和三重指数平滑法[22]。该模型能够捕捉到数据中的趋势和季节性变化, 适用于处理月度数据、季度数据等时间序列中的固定周期的波动行为, 从而提供相对准确的预测。可以使用ets()函数拟合指数模型, 根据时间序列数据自动选择合适的模型类型。
1.2.2 LPro集成模型本研究利用不同单一模型(ARIMA模型、线性趋势季节模型、Prophet模型和指数平滑模型)的MAPE作为衡量指标, 通过分析2019—2022年的历史预测表现, 为集成模型分配权重。集成模型的预测值是基于两个经过权重分配的模型的加权组合, 最终选出线性趋势季节模型和Prophet模型, 构建了LPro集成模型。经过评估, 该集成模型表现出更优的预测效果, 提高了时间序列预测的精度。其中, 权重分配的原则为表现越优异的模型获得更高的权重, 从而在最终预测中占据更大的影响力。LPro集成模型的公式如下:
| $ \hat{\mathrm{P}}=\frac{\left(1-\mathrm{MAPE}_{\text {线性 }}\right)}{\left(\mathrm{MAPE}_{\text {线性 }}+\mathrm{MAPE}_{\text {Prophet }}\right)} \hat{\mathrm{y}}_{\text {线性 }}+\frac{\left(1-\mathrm{MAPE}_{\text {Prophet }}\right)}{\left(\mathrm{MAPE}_{\text {线性 }}+\mathrm{MAPE}_{\text {Prophet }}\right)} \hat{\mathrm{y}}_{\text {Prophet }} $ |
其中, $\hat{\mathrm{P}}$为未来最终预测数据值, MAPE线性和MAPEProphet分别为基于历史数据计算的平均绝对百分比误差, $\hat{y}$线性为使用线性趋势季节模型预测未来数据值, $\hat{y}$Prophet为使用Prophet模型预测的未来数据值。
1.3 模型性能评价指标为比较不同模型的预测性能, 本研究采用了多种统计指标从不同角度评估了模型的性能, 包括平均绝对百分比误差(mean absolute percentage error, MAPE)、均方根误差(root mean square error, RMSE)、平均绝对误差(mean absolute error, MAE)、以及决定系数R2。MAPE将不同模型的数据集的预测误差进行比较, 是衡量预测结果误差的常用指标; RMSE是衡量预测值和实际观测值之间差异的常用度量, 对大的误差给予更大的惩罚; MAE为另一种常用的度量预测精度的方法, 与RMSE相比, MAE对大的误差不太敏感; R2用于衡量模型拟合数据的优良程度。这些指标能够有效地量化预测值与实际观测值之间的差异, 以及模型在数据解释上的能力, 从而为模型的选择和优化提供依据。各模型的预测值95%置信区间(95%CI)通过以下方法计算: 对于ARIMA模型和线性趋势季节模型, 使用R语言forecast包的forecast()函数自动生成; 对于Prophet模型, 使用其predict()函数输出的yhat_lower和yhat_upper; 对于指数平滑模型, 使用forecast()函数的预测区间; 对于LPro集成模型, 基于组成模型的预测方差加权计算得出。置信区间宽度反映了预测的不确定性, 区间越窄表明预测越稳定。
2 结果 2.1 邯郸市院前急救的基本情况2019—2023年邯郸市院前急救出车次数累计289 949例, 呈现逐年增长趋势。其中, 2019年出车35 527例, 2020年52 015例(较2019年增长46.42%), 2021年61 836例(较2020年增长18.88%), 2022年66 540例(较2021年增长7.61%), 2023年74 031例(较2022年增长11.26%), 2019—2022年复合年均增长率为23.27%。
本研究采用2019—2022年数据(215 918例, 年均53 980例)作为训练集进行模型构建, 2023年数据(74 031例)作为验证集评估模型预测性能。训练集中, 按月份统计显示10月月均出车约5 108例; 2月出车最少, 为13 870例; 2~10月呈现明显上升趋势(图 1)。训练集月均出车4 498次, 验证集月均出车6 169次, 两组数据均呈现2月出车最少、10月出车最多的季节性特征, 且出车次数呈持续增长趋势, 具有可比性。
|
| 图 1 2019—2022年不同月份有效出车情况 Fig 1 Effective vehicle trips in different months from 2019 to 2022 |
|
|
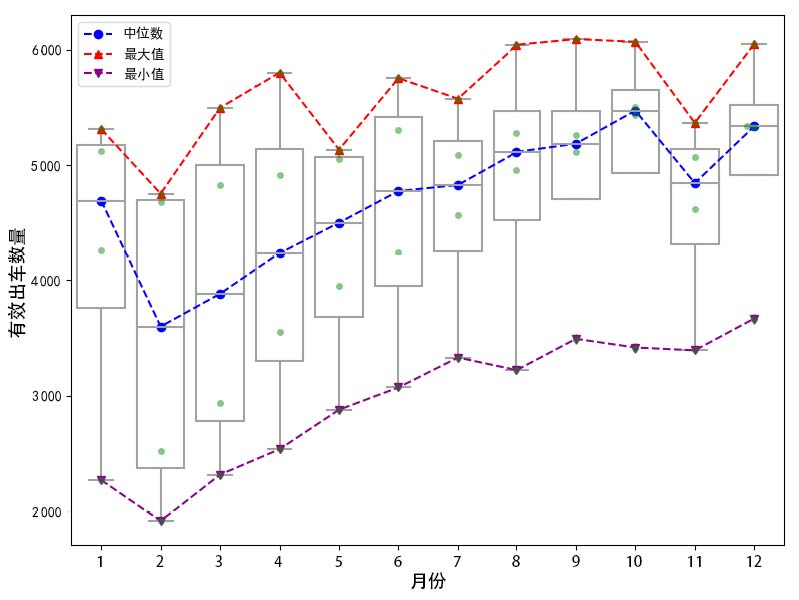
为了更精准预测邯郸市院前急救的需求趋势, 本研究使用R语言stl()函数将时间序列数据分解为季节性、长期趋势和残差组件(主要为随机波动)。如图 2所示, 邯郸市院前急救存在明显季节性特征, 2019—2022年院前急救出车次数呈逐年增加的长期趋势。在移除季节性和长期趋势之后, 残差组件在大多数时间内波动较小, 但存在几个显著的尖峰或跌落, 可能反映了突发公共卫生事件或特殊时期的影响。总体而言, 该时间序列的上升趋势及季节性特征较为明显, 为时间序列模型的应用提供了良好基础。
|
| 图 2 2019—2022时间序列分解示意图 Fig 2 Schematic diagram of time series decomposition from 2019 to 2022 |
|
|
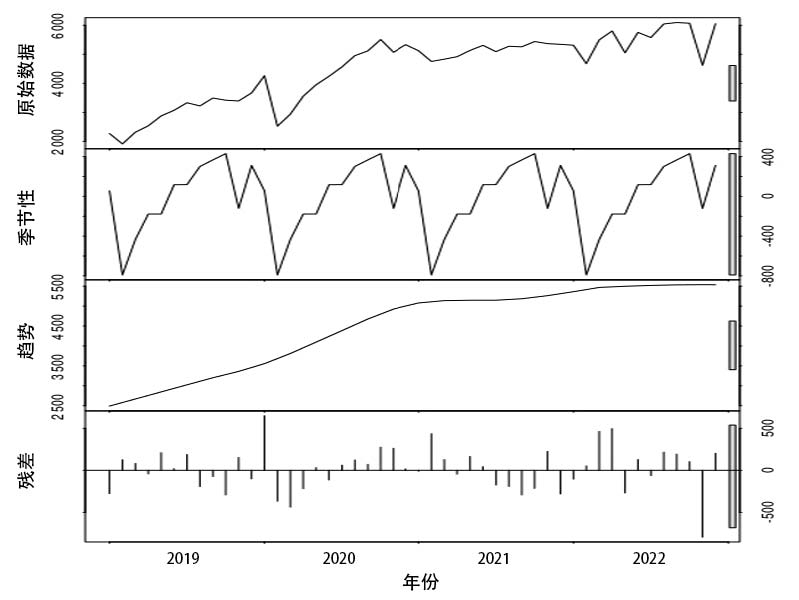
运用已自动选择最优模型ARIMA(0, 1, 1)(1, 0, 0)[12]对邯郸市2023年1—12月院前急救出车车次进行预测, 通过预测值和实际值的比较发现, 该模型预测出车车次比真实出车车次仅少预测502例, 超出比例仅0.68%, 预测出车总数和真实出车总数较为接近, 误差较小。ARIMA模型在预测2023年院前急救出车车次时, 在2月预测值和真实值误差较大, 如图 3A所示, 整体预测趋势和真实数据趋势较为一致, 但平均相对误差偏大达8.76%。
|
| 图 3 各模型预测值和实际值拟合图 Fig 3 Fitting diagram of predicted values and actual values for each model |
|
|
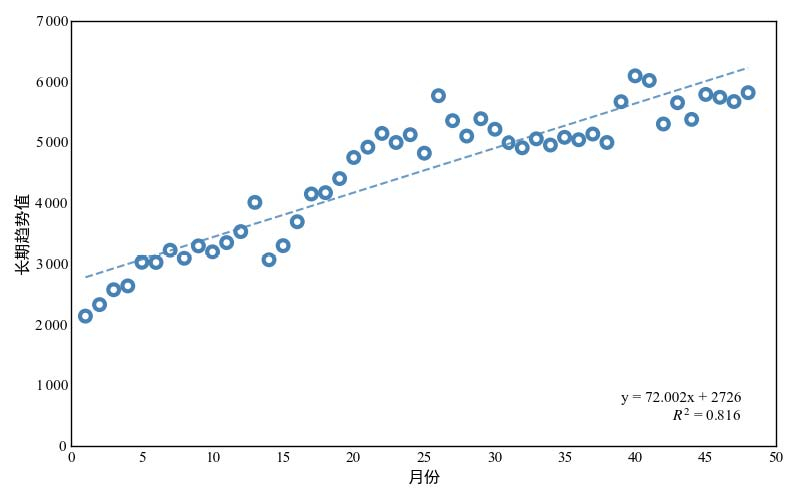
利用最小二乘法原理求解参数, 得到线性回归模型=72.002x+2726(图 4)。运用所构建的线性回归模型进行预测, 结果显示2023年邯郸市院前急救车辆预计出动总次数为79 923次, 这与长期的增长趋势相符。然而, 实际数据显示全年累计出动次数为74 031次, 比预测值多出5 892次, 超出比例7.37%, 平均相对误差9.83%, 预测趋势数据如图 3B所示, 关于线性趋势季节模型预测的详细数据可参见表 1。
|
| 图 4 消除季节变动后长期趋势及拟合线 Fig 4 Long-term trend and fitted line after eliminating seasonal variation |
|
|
| 月份 | 真实值 | ARIMA模型 | 线性趋势季节模型 | ||||
| 预测值 | 相对误差(%) | 95%CI | 预测值 | 相对误差(%) | 95%CI | ||
| 1 | 5 155 | 5 775 | 12.03 | 4 898~6 653 | 6 654 | 29.08 | 5 713~7 595 |
| 2 | 4 157 | 5 615 | 35.07 | 4 649~6 581 | 5 219 | 25.55 | 4 278~6 160 |
| 3 | 6 102 | 5 937 | 2.70 | 4 889~6 984 | 5 776 | 5.34 | 4 835~6 717 |
| 4 | 5 516 | 6 087 | 10.35 | 4 964~7 210 | 6 241 | 13.14 | 5 300~7 182 |
| 5 | 6 056 | 5 889 | 2.76 | 4 695~7 083 | 6 239 | 3.02 | 5 298~7 180 |
| 6 | 6 398 | 6 171 | 3.55 | 4 911~7 432 | 6 738 | 5.31 | 5 797~7 679 |
| 7 | 6 415 | 6 162 | 3.94 | 4 839~7 486 | 6 939 | 8.17 | 5 998~7 880 |
| 8 | 6 324 | 6 367 | 0.68 | 4 983~7 751 | 7 056 | 11.57 | 6 115~7 997 |
| 9 | 6 696 | 6 433 | 3.93 | 4 991~7 876 | 7 254 | 8.33 | 6 313~8 195 |
| 10 | 7 178 | 6 476 | 9.78 | 4 978~7 974 | 7 393 | 3.00 | 6 452~8 334 |
| 11 | 6 850 | 6 047 | 11.72 | 4 495~7 598 | 7 079 | 3.34 | 6 138~8 020 |
| 12 | 7 184 | 6 570 | 8.55 | 4 966~8 173 | 7 335 | 2.10 | 6 394~8 276 |
| 注: 相对误差=|预测值-真实值|/真实值×100% | |||||||
| 月份 | 真实值 | Prophet模型 | 指数模型 | Lpro集成模型 | ||||||
| 预测值 | 相对误差(%) | 95%CI | 预测值 | 相对误差(%) | 95%CI | 预测值 | 相对误差(%) | 95%CI | ||
| 1 | 5 155 | 5 979 | 15.98 | 5 433~6 542 | 5 901 | 14.47 | 4 681~7 120 | 6236 | 20.97 | 5 577~6 895 |
| 2 | 4 157 | 4 842 | 16.48 | 4 331~5 439 | 6 017 | 44.74 | 4 590~7 443 | 4985 | 19.92 | 4 326~5 644 |
| 3 | 6 102 | 5 613 | 8.01 | 5 075~6 156 | 6 133 | 0.51 | 4 519~7 748 | 5675 | 7.00 | 5 016~6 334 |
| 4 | 5 516 | 5 894 | 6.85 | 5 363~6 426 | 6 250 | 13.31 | 4 461~8 039 | 6026 | 9.25 | 5 367~6 685 |
| 5 | 6 056 | 5 653 | 6.65 | 5 089~6 210 | 6 366 | 5.12 | 4 412~8 320 | 5876 | 2.97 | 5 217~6 535 |
| 6 | 6 398 | 6 148 | 3.91 | 5 576~6 700 | 6 482 | 1.31 | 4 371~8 594 | 6372 | 0.41 | 5 713~7 031 |
| 7 | 6 415 | 6 215 | 3.12 | 5 646~6 817 | 6 599 | 2.87 | 4 335~8 863 | 6490 | 1.17 | 5 831~7 149 |
| 8 | 6 324 | 6 343 | 0.30 | 5 751~6 932 | 6 715 | 6.18 | 4 303~9 127 | 6614 | 4.59 | 5 955~7 273 |
| 9 | 6 696 | 6 144 | 8.24 | 5 590~6 674 | 6 832 | 2.03 | 4 275~9 388 | 6566 | 1.94 | 5 907~7 225 |
| 10 | 7 178 | 6 401 | 10.82 | 5 823~7 010 | 6 948 | 3.20 | 4 251~9 645 | 6778 | 5.57 | 6 119~7 437 |
| 11 | 6 850 | 6 208 | 9.37 | 5 607~6 733 | 7 064 | 3.12 | 4 228~9 901 | 6539 | 4.54 | 5 880~7 198 |
| 12 | 7 184 | 6 363 | 11.43 | 5 819~6 953 | 7 181 | 0.04 | 4 207~10 154 | 6732 | 6.29 | 6 073~7 391 |
| 注: 相对误差=|预测值-真实值|/真实值×100% | ||||||||||
使用R包prophet预测邯郸市2023年院前急救车次, 基于Prophet模型的预测结果显示, 2023年邯郸市院前急救车辆预计出动总次数为71 803次, 比真实数据少出2 228次, 占年度预测出车车次3.10%, 平均相对误差为8.43%。在9月—12月份预测数据和真实数据有些差异, 但趋势保持一致, 如图 3C所示。关于Prophet模型预测2023年每月的具体与实际出动次数的详细数据, 如表 1所示。
2.2.4 指数模型预测情况拟合指数平滑预测模型最佳为ETS(M, A, N), 预测结果显示, 预测出车车次逐月递增, 预测年出车车次量为78 488次, 较真实数据多预测4 457车次, 超出比例5.68%。该模型平均相对误差8.08%, 在上述现有模型中的相对误差最低, 但呈现直线上升趋势, 和真实数据的趋势明显不同, 如图 3D所示。
2.3 LPro集成模型预测情况基于线性趋势季节模型和Prophet模型预测出的数据与真实数据计算模型的MAPE值, 模型MAPE值分别为8.76%、5.46%, 模型分配的权重值约为0.38和0.62。使用LPro集成模型预测结果显示, 预计全年的累计出车次数为74 889次。实际记录的出车次数为74 031次, 预测数据与实际数据相差858车次, 平均相对误差仅为7.05%。LPro集成模型预测每月出车车次情况, 如表 1所示。
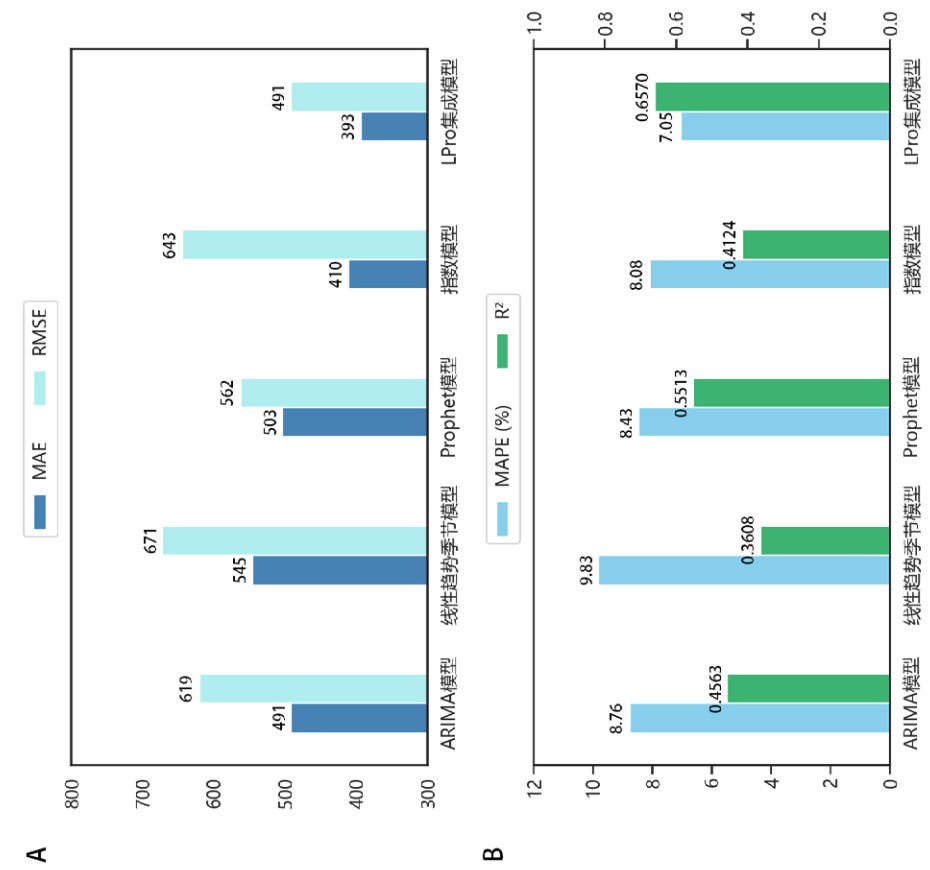
2.4 模型比较首先, 从相对误差来看, 如表 1所示了各模型对2023年12个月的预测值及相对误差。ARIMA模型在2月预测误差最大(35.07%), 线性趋势季节模型在1月和2月预测误差均超过25%, Prophet模型和LPro集成模型的各月相对误差波动较小且均控制在21%以内, 其中LPro集成模型在9个月份的相对误差低于10%, 显示出更好的预测稳定性和准确性。其次, 从置信区间方面来看。如表 1所示了各模型对2023年12个月的预测值及其95%CI。指数模型的预测不确定性最大(95%CI跨度平均为4 309), 其次为ARIMA模型(95%CI跨度平均为2 545), 然后为线性趋势季节模型(95%CI跨度平均为1 882), Prophet模型和Lpro集成模型的置信区间宽度相近(平均约1 124和1 318), 表明其预测稳定性较好。如图 5A、5B所示, LPro集成模型表现最佳, 其MAPE指标相比于表现次佳的Prophet模型, 误差降低了约1.38%, 相较于最差的线性趋势季节模型, 误差降低了约2.78%。LPro集成模型RMSE指标, 相比于RMSE最高的线性趋势季节模型, 误差减少了180, 相比于ARIMA模型, 误差减少了128。LPro集成模型的MAE指标显著低于其他模型, 特别是与线性趋势季节模型相比, 误差减少了152, 与ARIMA模型相比减少了98。LPro集成模型的R2显著高于其他模型, 尤其是与表现最差的线性趋势季节模型相比, 提升了29.62%, 与Prophet模型相比, 提升了10.57%。这些结果表明, LPro集成模型有效地结合了多模型的优点, 显著提高了预测的准确性和可靠性。
|
| 图 5 各模型指标比较 Fig 5 Comparison of model indicators |
|
|
2019—2023年, 邯郸市院前急救服务中的急救出车次数逐年上升, 出车车次增长近两倍, 提示该地区对院前急救需求迫切, 值得注意的是, 北京市院前急救需求也存在类似趋势, 2018—2022年急救车出车次数也增长近两倍[9]。本研究还发现院前急救出车车次的变化呈现明显的季节性: 2月和11月出车车次有明显下降趋势, 2~7月集中趋势逐步上升, 8~10月及12月有效出车情况呈现类似趋势, 2月份和11月份急救车次有所下降, 其中2月达到年度最低值。相对地, 在8~10月及12月, 急救需求则显著增高。从年度增长趋势来看, 2019—2021年间急救出车车次的增长较为迅速, 而2021—2022年的增长则相对缓慢, 这种变化可能受到了疫情的影响。2019—2022年的残差波动幅度相对一致, 没有明显的变化趋势, 但存在一些较大的正负残差点, 可能是特定事件或未被趋势和季节性分量捕捉到的其他影响因素。
3.2 时间序列模型ARIMA模型和线性趋势季节模型本质相同, 只能捕捉线性关系, 而不能捕捉非线性关系。Prophet模型能够自动检测并拟合数据中的非线性趋势, 通过灵活的趋势变化和季节性分析来适应时间序列数据的变动[23], 提供更为准确的预测。指数模型是在移动平均法基础上发展起来的, 这与线性趋势季节模型计算长期趋势相一致, 尽管选择出的最优指数模型平均相对误差较小, 但该模型没有考虑季节性变化, 导致呈现线性上升趋势, 拟合数据和真实数据趋势不符。ARIMA模型、线性趋势季节模型和Prophet模型拟合趋势和院前急救出车车次趋势基本一致, 只是波动幅度有所不同, 其中线性趋势季节模型构建回归方程拟合度高达0.816, 在预测未来数据拟合度有所降低, 可能受到异常值、随机波动的影响。
3.3 LPro集成模型多模型加权的目的是充分利用不同预测模型之间的差异性, 提高整体预测模型的泛化能力和鲁棒性[24]。通过综合不同模型的预测能力和特点, 平衡各自的强弱, 以达到降低单一模型误差的目的。本研究将多个模型进行集成, 最终基于线性趋势季节模型和Prophet模型开发了LPro集成模型, 有效地降低了预测偏差。LPro集成模型较单一模型相比, 在各个指标均表现最优, 相对于ARIMA模型的MAPE、RMSE、和MAE分别相对下降了24.26%、26.07%、24.94%;线性趋势季节模型的MAPE、RMSE、和MAE分别相对下降了39.43%、36.66%、38.68%;Prophet模型的MAPE、RMSE、和MAE分别相对下降了19.57%、14.46%、27.99%;指数模型的MAPE、RMSE、和MAE分别相对下降了14.61%、30.96%、4.33%。由此可以得出结论, LPro集成模型比单一模型预测误差都有所降低, 更具优势的预测精度。相关研究者使用组合模型预测铁路行车事故数, 得出组合预测模型的预测结果比单一预测模型的预测结果更好, 这与本研究结论一致[25]。组合模型通常能够提高预测的稳定性, 并减少依赖单一模型可能带来的风险。
综上所述, 使用LPro集成模型具有更好的预测结果。通过运用时间序列预测模型, 能够更精确地预测急救服务需求的变化趋势, 优化急救资源的分配, 显著提高急救服务的响应效率和居民的生活质量, 展示了数据驱动方法在公共卫生领域的巨大潜力和价值。
利益冲突 所有作者声明无利益冲突
作者贡献声明 田丰和路赛丛负责研究设计、研究指导和论文撰写; 毕程程和李朋辉负责论文撰写与修订; 张海方、杨振杰和张龙强负责数据收集; 赵婷婷、王贤、谷佳璇、周世涛、靳增军、王珍、赵菲菲和苏县辉负责数据整理和资料整理; 所有作者均已阅读并同意论文的最终版本
| [1] | Huang W, Wang TB, He YD, et al. Trends and characteristics in pre-hospital emergency care in Beijing from 2008 to 2017[J]. Chin Med J (Engl), 2020, 133(11): 1268-1275. DOI:10.1097/CM9.0000000000000770 |
| [2] | Wilson MH, Habig K, Wright C, et al. Pre-hospital emergency medicine[J]. Lancet, 2015, 386(10012): 2526-2534. DOI:10.1016/S0140-6736(15)00985-X |
| [3] | Setzler H, Saydam C, Park S. EMS call volume predictions: a comparative study[J]. Comput Oper Res, 2009, 36(6): 1843-1851. DOI:10.1016/j.cor.2008.05.010 |
| [4] | Yang PY, Cheng PF, Zhang N, et al. Statistical machine learning models for prediction of China's maritime emergency patients in dynamic: ARIMA model, SARIMA model, and dynamic Bayesian network model[J]. Front Public Health, 2024, 12: 1401161. DOI:10.3389/fpubh.2024.1401161 |
| [5] | Chen AY, Lu TY, Ma MH, et al. Demand forecast using data analytics for the preallocation of ambulances[J]. IEEE J Biomed Health Inform, 2016, 20(4): 1178-1187. DOI:10.1109/JBHI.2015.2443799 |
| [6] | Fattah J, Ezzine L, Aman Z, et al. Forecasting of demand using ARIMA model[J]. Int J Eng Bus Manag, 2018, 10: 1847979018808673. DOI:10.1177/1847979018808673 |
| [7] | Rostami-Tabar B, Browell J, Svetunkov I. Probabilistic forecasting of hourly emergency department arrivals[J]. Health Syst (Basingstoke), 2023, 13(2): 133-149. DOI:10.1080/20476965.2023.2200526 |
| [8] | Peng JY, Zeng XY, Huang S, et al. Trends of hospitalisation among new admission inpatients with oesophagogastric variceal bleeding in cirrhosis from 2014 to 2019 in the Affiliated Hospital of Southwest Medical University: a single-centre time-series analysis[J]. BMJ Open, 2024, 14(2): e074608. DOI:10.1136/bmjopen-2023-074608 |
| [9] | 邓贵芳, 孙涛, 耿聆, 等. 基于时间序列模型的北京市院前急救出车车次预测分析[J]. 中国急救复苏与灾害医学杂志, 2024, 19(5): 587-590. DOI:10.3969/j.issn.1673-6966.2024.05.007 |
| [10] | Yang WJ, Su AN, Ding LP. Application of exponential smoothing method and SARIMA model in predicting the number of admissions in a third-class hospital in Zhejiang Province[J]. BMC Public Health, 2023, 23(1): 2309. DOI:10.1186/s12889-023-17218-x |
| [11] | Luo ZX, Jia XC, Bao JZ, et al. A combined model of SARIMA and prophet models in forecasting AIDS incidence in Henan Province, China[J]. Int J Environ Res Public Health, 2022, 19(10): 5910. DOI:10.3390/ijerph19105910 |
| [12] | Ab Rashid MA, Ahmad Zaki R, Wan Mahiyuddin WR, et al. Forecasting new tuberculosis cases in Malaysia: a time-series study using the autoregressive integrated moving average (ARIMA) model[J]. Cureus, 2023, 15(9): e44676. DOI:10.7759/cureus.44676 |
| [13] | 李霞, 张瑜, 朱勤忠. 上海市中心城区院前急救业务量的预测和分析[J]. 中国医院统计, 2016, 23(1): 44-46. DOI:10.3969/j.issn.1006-5253.2016.01.014 |
| [14] | Arslan S. A hybrid forecasting model using LSTM and Prophet for energy consumption with decomposition of time series data[J]. PeerJ Comput Sci, 2022, 8: e1001. DOI:10.7717/peerj-cs.1001 |
| [15] | Wang ZX, Zhang WY, Wu T, et al. Time series models in prediction of severe fever with thrombocytopenia syndrome cases in Shandong province, China[J]. Infect Dis Model, 2024, 9(1): 224-233. DOI:10.1016/j.idm.2024.01.003 |
| [16] | Agyemang EF, Mensah JA, Ocran E, et al. Time series based road traffic accidents forecasting via SARIMA and Facebook Prophet model with potential changepoints[J]. Heliyon, 2023, 9(12): e22544. DOI:10.1016/j.heliyon.2023.e22544 |
| [17] | Yu GC, Feng HF, Feng S, et al. Forecasting hand-foot-and-mouth disease cases using wavelet-based SARIMA-NNAR hybrid model[J]. PLoS One, 2021, 16(2): e0246673. DOI:10.1371/journal.pone.0246673 |
| [18] | Zhao Z, Zhai M, Li G, et al. Study on the prediction effect of a combined model of SARIMA and LSTM based on SSA for influenza in Shanxi Province, China[J]. BMC Infectious Diseases, 2023, 23(1): 71. DOI:10.1186/s12879-023-08025-1 |
| [19] | Benvenuto D, Giovanetti M, Vassallo L, et al. Application of the ARIMA model on the COVID-2019 epidemic dataset[J]. Data Brief, 2020, 29: 105340. DOI:10.1016/j.dib.2020.105340 |
| [20] | 蒋莹, 徐哲, 程庆林, 等. 季节趋势模型在犬伤门诊就诊人次数预测中的探究[J]. 医学动物防制, 2024, 40(6): 559-562. DOI:10.7629/yxdwfz202406008 |
| [21] | 李威, 鲁铁定, 贺小星, 等. 基于Prophet-RF模型的GNSS高程坐标时间序列预测分析[J]. 大地测量与地球动力学, 2021, 41(2): 116-121. DOI:10.14075/j.jgg.2021.02.002 |
| [22] | Xu WZ, Shao ZH, Lou HL, et al. Prediction of congenital heart disease for newborns: comparative analysis of Holt-Winters exponential smoothing and autoregressive integrated moving average models[J]. BMC Med Res Methodol, 2022, 22(1): 257. DOI:10.1186/s12874-022-01719-1 |
| [23] | Taylor SJ, Letham B. Forecasting at scale[J]. Am Stat, 2018, 72(1): 37-45. DOI:10.1080/00031305.2017.1380080 |
| [24] | Kaur J, Parmar KS, Singh S. Autoregressive models in environmental forecasting time series: a theoretical and application review[J]. Environ Sci Pollut Res Int, 2023, 30(8): 19617-19641. DOI:10.1007/s11356-023-25148-9 |
| [25] | Panigrahi S, Behera HS. A hybrid ETS–ANN model for time series forecasting[J]. Eng Appl Artif Intell, 2017, 66: 49-59. DOI:10.1016/j.engappai.2017.07.007 |
 2025, Vol. 34
2025, Vol. 34